Методика реализации стохастической линии в 7 классе

Какой размер обуви наиболее распространен?

Исходя из вопроса, делаем вывод, что в данной задаче нам требуется найти моду ряда размеров, то есть узнать, какой размер пользуется большим спросом. Таблица позволяет быстро это сделать.

Бензоколонка работает круглосуточно без выходных. За январь выручка составила 71 796 000 р. Какова была в январе средняя выручка за сутки?

В данной задаче необходимо понимать, что требуется найти. Раз требуется найти среднюю выручку, то делаем вывод, что необходимо найти среднее арифметическое. Но до этого учащиеся имели дело непосредственно с рядом данных. В данной ситуации мы имеем, что сумма выручки за 31 день составила 71 796 000 рублей. Тогда мы можем посчитать среднее арифметическое (71 796 000 : 31) = 2 316 000, это и будет средняя выручка за сутки.

Среднее арифметическое ряда, состоящего из десяти чисел, равно 15. К этому ряду приписали число 37. Чему равно среднее арифметическое нового ряда чисел?

Так как среднее арифметическое ряда чисел равно 15, а число его членов равно 10, то сумма членов равна 15∙10, т.е. 150. После приписывания числа 37 сумма стала ровно 150+37, т.е. 187, а число членов ряда оказалось равным 11. значит, среднее арифметическое нового ряда равно 187 : 11, т.е. равно 17.

Учащиеся должны уметь вычислять статистические характеристики по данным, представленным в таблице.

При изучении качества продукции выпущенной цехом, определяли число бракованных деталей в каждом из 50 произвольным образом выбранных ящиков с одинаковым числом деталей. Результаты проверки записали в виде таблицы:

Найдите среднее арифметическое, размах и моду ряда данных.

Сначала выпишем упорядоченный ряд данных о количестве бракованных деталей в ящиках. Из таблицы мы вычисляем, что наш ряд содержит 8 нулей, 22 единицы и т.д.

0 … 0 1… 1 2…2 3 … 3 4 4.

8 22 13 5

Таким образом, чтобы вычислить среднее арифметическое, необходимо, вычислить сумму всех его членов, а количество всех членов ряда известно из условия задачи (50 ящиков). Сумма всех членов будет равна 0*8+1*22+2*13+3*5+4*2=71, а количество всех членов будет 50, тогда среднее арифметическое будет 71:50 = 1,42, т.е. чаще встречаются ящики, в которых может быть одна бракованная деталь. Об этом же говорит нам и мода, которая равна 1.

Чтобы вычислить размах, необходимо знать наибольшее и наименьшее значение, т.е. какое наибольшее и наименьшее число бракованных деталей может попасться в ящике, из таблицы мы видим, что это 0 и 4. тогда размах равен 4.

Мода тоже очень легко вычисляется по таблице, так как сразу видно, что наибольшее число ящиков с одной бракованной деталью.

Не менее важным является и умение вычислять статистические характеристики по данным представленными в диаграмме.

На диаграмме представлены данные о числе болельщиков, посетивших футбольные матчи на стадионе «Динамо» за последний месяц. Найдите размах посещаемости и среднюю посещаемость матча, округлив ее до сотен.

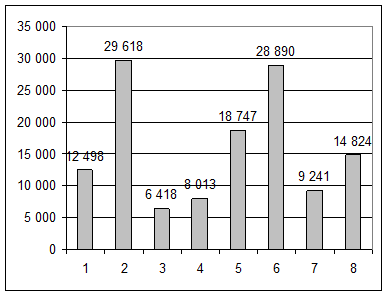
По диаграмме мы можем сразу вычислить наибольшее и наименьшее значения и найти размах. Средняя посещаемость для данного случая это среднее арифметическое ряда этих данных.

К 7 классу учащиеся уже должны иметь навыки систематического перебора и быть знакомы с основными методами подсчета возможных вариантов. В 7 классе продолжаем решать задачи на подсчет возможных вариантов различными способами, а также вводим понятие перестановки.

Раньше учащиеся уже сталкивались с перестановками, когда подсчитывали сколькими способами можно упорядочить несколько (2,3 или 4) элементов, но само понятие перестановки еще не вводилось.

На данный момент мы уже знаем, количество перестановок для 2, 3 и 4-ех элементных множеств.

В турнире участвуют четыре человека. Сколькими способами могут быть распределены места между ними?

Решим эту задачу, используя правило умножения. Первое место может занять любой из четырех участников. При этом второе место может занять любой из трех оставшихся, третье – любой из двух оставшихся, а на четвертом месте остается последний участник. Значит, места между участниками могут быть распределены 4*3*2*1 = 24 способами.