Информационная функция

Согласно А.Бирнбауму количество информации, обеспеченное j-м заданием теста в данной точке θi - это величина, обратно пропорциональная стандартной ошибке измерения данного значения θi с помощью j-го задания. Для описания информации, соответствующей заданию вводится информационная функция I(θ)

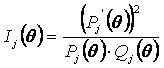
Для однопараметрической модели Pj’ = 1,7PjQj, тогда

Ij(θ) = 2,89Pj(θ)Qj(θ), где Qj(θ) = 1 - Pj(θ)-вероятность неверного ответа на j-е задание. Поскольку

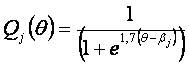
то выражение для информационной функции

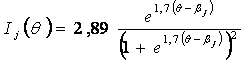
Построим информационную функцию для однопараметрической модели

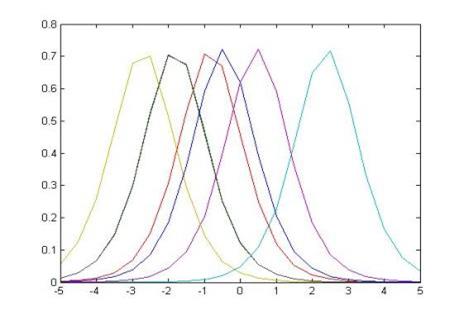
Информационные функции обладают свойством аддитивности

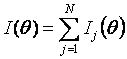
Это означает, что можно построить информационную функцию всего теста

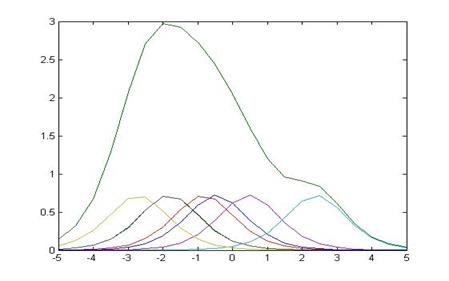
Информационная функция теста должна иметь один четко выраженный максимум. Если это не так, то тест нуждается в доработке, в него необходимо добавить задания с трудностями, соответствующими областями провала информационной функции теста.

Характеристические кривые некоторых заданий, а именно 2 и 7; 3 и 8 перекрываются. В связи с этим 7 и 8 задания могут быть удалены из теста без ущерба его измерительным свойствам.

Этот тест явно нуждается еще в заданиях с трудностями в области +1.5 логит. Улучшения информационной функции теста можно добиться и не изменяя числа заданий в нем. Для этого необходимо сдвинуть задание №5 влево, то есть уменьшить его трудность.