Методика реализации стохастической линии в 6 классе

Такой способ подсчета называется правилом умножения, он возможен, если дерево возможных вариантов является «правильным»: из каждого узла выходит одно и тоже число веток.

От турбазы к горному озеру ведут 4 тропы. Сколькими способами туристы могут отправиться в поход к озеру, если они не хотят спускаться по той же тропе, по которой поднимались?

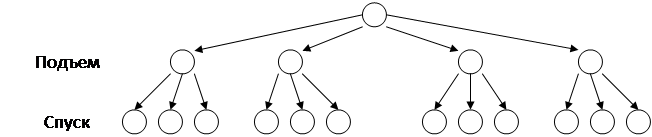Занумеруем тропы числами от 1 до 4 и построим дерево возможных вариантов:

Чтоб подняться у нас есть 4 тропы (4 варианта) и на каждый из них есть по 3 оставшихся тропы (3 варианта), чтоб спуститься, т.е. 4*3=12 маршрутов подхода к озеру. А теперь представим, что к озеру ведут не 4, а 10 троп. Сколько в этом случае существует маршрутов, если по-прежнему решено спускаться не по той тропе, по которой поднимались. Изобразить дерево возможных вариантов в такой ситуации очень сложно. Гораздо легче решить эту задачу с помощью рассуждений. Подняться к озеру можно по любой из 10 троп, а спускаться по любой из оставшихся 9 троп. Таким образом, всего получим 10*9=90 различных маршрутов похода.

Обе эти задачи мы решили, используя правило умножения, которое звучит следующим образом: пусть необходимо выполнить к независимых действий, если первое действие мы можем выполнить п1 способами, после чего второе действие можем выполнить п2 способами и т.д. до k-го действия, которое можно выполнить пk способами, тогда выполнить все k действия в указанном порядке можно п1∙ п2∙…∙ пk способами. Обратить внимание, что, применяя правило умножения, мы учитываем порядок действий. То есть правило умножения применяется для подсчета упорядоченных наборов.

Рассмотрим две задачи:

1) Сколькими способами из класса, в котором учатся 30 школьников, можно выбрать капитана команды для математических соревнований и его заместителя?

На роль капитана может быть выбран любой из 30 учащихся, а его заместитель – любой из 29 оставшихся учеников. Таким образом, получаем 30∙29 = 870 способов.

2) Сколькими способами из класса, в котором учатся 30 школьников, можно выбрать двоих для участия в математической олимпиаде?

Нам не важно, кто капитан, а кто заместитель, нам нужны всего лишь два участника, поэтому получаем, что у нас каждая пара учащихся в произведении повторяется два раза. Поэтому ответом для второй задачи будет (30∙29):2.

Еще одним способом подсчета комбинаторных наборов является использование правила суммы.

Из класса нужно выделить одного дежурного, мальчика или девочку. Сколько существует способов для выбора дежурного, если в классе 22 девочки и 18 мальчиков?

Выбрать одну девочку из 22 мы можем 22-мя способами, а одного мальчика из 18 можно 18-тью способами. Тогда выбрать одного дежурного мальчика или девочку можно (18+22) способами.

Для подсчета вариантов мы использовали здесь правило суммы, которое можно сформулировать так: если два действия взаимно исключают друг друга, причем одно из них можно выполнить п способами, а другое – m способами, то какое-либо одно из них можно выполнить n+m способами. В нашем примере действия исключают друг друга, так как мы должны выбрать либо мальчика из одного множества, либо девочку из другого.

В 6 классе продолжаем вероятностную линию. Начинаем с повторения, что такое случайное событие, определение его достоверности (невозможное, достоверное, маловероятное). Новой задачей становится формирование умения оценивать вероятности двух и более событий (более или менее вероятно).

Полезно рассматривать задачи, в которых при ответе на вопросы необходимо опираться на свою интуицию. Можно рассматривать реальные жизненные ситуации, чтоб учащиеся видели непосредственную связь изучаемого с действительностью.

Вы купили в магазине телевизор, на который фирма-производитель дает два года гарантии. Какие из следующих событий невозможные, случайные, достоверные:

А) телевизор не сломается в течении года.

Б) телевизор не сломается в течении двух лет.

В) в течение двух лет вам не придется платить за ремонт телевизора.

Г) телевизор сломается на третий год.

Здесь нужно обратить внимание учащихся, что первые два события случайные, так как, во-первых, гарантия фирмы производителя вовсе не обозначает, что в течение двух лет телевизор будет работать идеально, а во-вторых, можно рассмотреть и тот случай, когда телевизор может сломаться по вине покупателя. Событие Г также является случайным, так как нельзя говорить, что телевизор обязательно сломается после того, как закончится срок гарантии.