Методика реализации стохастической линии в 8 классе

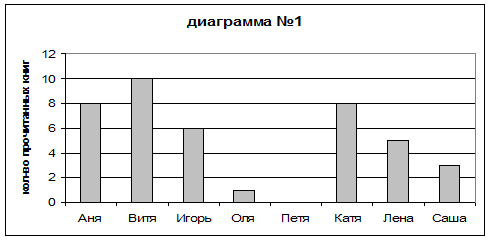
а) Кто из ребят прочел больше всех книг?

б) найдите размах этих данных.

в) Кто за летние каникулы не прочел ни одной книги?

г) Найдите среднее арифметическое этого ряда данных.

д) Найдите медиану этого ряда данных.

В предыдущих классах мы рассмотрели, как можно оценивать вероятность, исходя их статистических данных. Такая вероятность приближенно равна частоте наступления интересующего нас события при проведении большого числа одинаковых случайных экспериментов. Но частота дает лишь приближенное значение вероятности. И кроме того, не всегда реально осуществить такую серию экспериментов.

Существуют и другие способы вычисления вероятностей. Если все исходы случайного эксперимента равновероятны, тогда вероятности каждого такого исхода можно подсчитать, не проводя экспериментов. Примером является подбрасывание монеты. Этот эксперимент имеет два исхода – «орел» и «решка», и они равновероятны. Тогда можно сказать, что вероятность каждого из них равна ½, почти такой же результат получен и при проведении экспериментов. Аналогично для «правильного» кубика, все шесть исходов равновозможны, тогда вероятность каждого из них равна 1/6.

Какова вероятность того, что при бросании правильного кубика выпадет четное число очков?

Мы знаем, что при бросании кубика возможны 6 равновероятных исходов. При этом только три из них приводят к наступлению события «выпадет четное число очков». Поэтому вероятность такого события равна 3/6 = 1/2.

Исходы наступления события, для которого вычисляем вероятность, будем называть благоприятными. И дадим такое определение вероятности:

Вероятностью Р наступления случайного события А называется отношение m/n, где п – число всех возможных исходов эксперимента, а m – число всех благоприятных исходов: Р(А) = т/п.

Это классическое определение вероятности.

Из 25 экзаменационных билетов по геометрии ученик успел подготовить 11 первых и 8 последних билетов. Какова вероятность того, что на экзамене ему достанется билет, который он не подготовил?

Общее число равновозможных исходов при выборе билетов на экзамене равно 25. Пусть А – событие «учащемуся достался билет, к которому он не готов». Число таких исходов равно 25-(11+8) = 6. значит Р(А) = 6/25 = 0,24.

Также рассмотрим задачи, в которых для подсчета числа благоприятных или всех исходов необходимо воспользоваться комбинаторными формулами.

На трехместную скамейку произвольным образом садятся двое мужчин и женщина. Какова вероятность того, что мужчины окажутся рядом?

Количество всех возможных исходов – это число перестановок трех элементов, а оно равно 3! = 6. Пусть А - событие «мужчины оказались рядом», количество благоприятных исходов для этого события равно четырем (когда оба сидят с одного края – 2 варианта и аналогично для другого тоже два варианта). Таким образом Р(А) = 4/6 = 2/3.

Кроме статистического и классического определений вероятности существует еще геометрическая вероятность. Рассмотрим следующий пример. На квадратном столе выделен черный квадратик. Как определить вероятность того, что фишка попадет в черный квадратик, если ее бросить на стол наугад.

Эта вероятность равно отношению площади черного квадрата к площади поверхности стола. Если, например, площадь стола равна 0,6м², а площадь черного квадрата – 0,04 м², то Р = 0,04/0,6 = 1/15.

Стрелок, не целясь, стреляет в треугольную мишень (рис.1) и попадает.

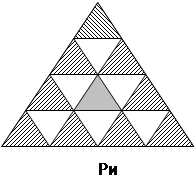Какова вероятность того, что он попадет в «тройку»? «двойку»? «единицу»?