Классические шкалы оценки знаний

По другой версии, коэффициент надёжности определяется как

,

где — дисперсия ошибок измерения, — дисперсия набранных баллов, т. е. время в таком определении коэффициента надёжности вообще не упоминается. Топ 8 оконных вентиляторов.

Сомнительность подобных вычислений с математической точки зрения связана с тем, что исходные данные изначально получены по шкале баллов, на которой бывает задано отношение порядка, и даже линейного порядка, но не определены арифметические операции. Следовательно, сложение и вслед за ним вычисление средних, взвешенных средних, дисперсий и корреляций на шкале баллов не определено. Ещё одно предположение, понятное с прагматической точки зрения, но с явно неадекватным теоретическим обоснованием, сводится к утверждениям о нормальном распределении ответов и, следовательно, с распределением «сырых баллов» на шкале действительных чисел. Предположение о логнормальном распределении тех же баллов часто кажется более правдоподобным, но содержательно обычно тоже не обосновывается. Эти предположения позволяют использовать при статистической обработке результатов хорошо известные методы, но математическая корректность всех последующих вычислений после этого предположения не обсуждается.

В литературе широко обсуждаются многие проблемы традиционного подхода к построению шкал (метрик) знаний как баллов за выполнение некоторых специально подобранных наборов заданий.

Прежде всего, практически невозможно доказать test-to-test- и intertest-валидность, следовательно, вопрос о сравнении и тем более об общем учёте результатов измерений, выполненных по разным методам, остаётся открытым.

Многократно отмечены «эффекты края», т. е. относительная устойчивость результатов ближе к медиане распределения ответов и неустойчивые результаты по краям этого распределения, что обычно объясняется возрастанием роли инородных факторов как в «нижней», так и в «верхней» части распределения. В качестве борьбы с этими эффектами обычно предлагается эмпирически обоснованная рекомендация задать некоторый «доверительный квантиль» распределения , обычно предлагается принять , или , и при попадании ответа ниже или выше вносить поправки на нестабильность, главным образом, завышать полученные оценки по эмпирически подобранным поправочным формулам.

В случае закрытых вопросов возможны ситуации случайного угадывания, для коррекции данных в этом случае предлагается вносить поправки вида

,

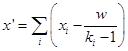где — результат после коррекции, — результат (в баллах или другим шкалам) ответа на -й вопрос до коррекции, — количество возможных ответов на -й вопрос, w — количество невыполненных заданий в серии измерений. Эта формула обосновывается эмпирически, в частности, обсуждается вопрос о целесообразности учёта в этой формуле невыполненных заданий, для которых соответствующее значение , что уменьшает значение , и идут дискуссии о содержательном смысле подобных поправок.