Классические шкалы оценки знаний

В целом, метрики качества знаний при классическом подходе обоснованы статистической калибровкой методов по соответствующей популяции. Со времён создания IQ метрологическое обоснование измерений знаний проводится по распределениям баллов, вычисленных по соответствующему контингенту респондентов. Например, указываются средние значения IQ по возрастным, социальным или профессиональным группам. Однако из разницы IQ непонятно, какие принципиальные отличия в структуре знаний различают эти группы.

Item Response Theory

В качестве средства обеспечения содержательной корректности метрик качества знаний в 50-е годы была предложена и с начала 80-х годов стала популярной Item Response Theory – IRT.

В IRT предполагается, что получаемые баллы оказываются внешними проявлениями результатов действия неких ненаблюдаемых переменных — латентных параметров, и ставится задача оценить эти параметры по результатам выполненным измерениям.

Первоначальный вариант IRT связан с именем Г.Раша. В IRT результат измерения считается внешним проявлением латентной переменной, и ставится задача восстановить оценку латентной переменной по измерениям видимых переменных. Для -го испытуемого значение латентной переменной , обычно интерпретируемой как оценка готовности, и уровень трудности -го задания расположены на одной шкале, измеримы в сравнимых единицах, которые в этой теории называются логиты, и поэтому вычислима разность .

В IRT предполагается существование семейства функций вида

,

где — вероятность того, что -й испытуемый выполнит -е задание. Точный вид зависимости может меняться, в модели могут также могут дополнительные параметры. Таким образом, предполагается, что вероятность успеха зависит только от разницы между уровнем готовности и сложностью задания, при этом уровень готовности отдельных испытуемых и уровень сложности задания предполагаются независимыми как минимум в статистическом смысле.

При использовании логистической функции, можно определить вероятность успеха -го испытуемого при решении-го задания как

,

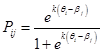где k — некий масштабный множитель, который используется для согласования различных шкал и моделей, и соответствующие интегральные характеристики сложности заданий для -го испытуемого и готовности испытуемого к решению-го задания.

Часто вместо модели Раша используется модель Фергюссона, в которой вместо логистической функции используется функция нормального распределения, тогда для совместимости этих двух моделей в модели Раша используется коэффициент . Принято считать, что модель Раша позволяет отделить трудности заданий от готовности испытуемых, т. е. от субъективной сложности заданий.