Классические шкалы оценки знаний

(2)

Масштабный множитель 1,7 используется для совместимости модели G.Rasch с моделью A.Fergusson, где вероятность правильного ответа на задание выражена интегралом нормального распределения что позволяет использовать вместо логистических кривых хорошо изученную интегральную функцию нормированного нормального распределения

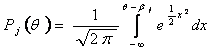(3)

Модель Раша носит название «1 Parametric Logistic Latent Trait Model» (1PL), а модель A.Fergusson - «1 Parametric Normal Ogive Model» (1PN). Поскольку модель Раша описывает вероятность успеха испытуемого как функцию одного параметра (θi - βj), то иногда ее называют однопараметрической моделью IRT.

Взаимодействие двух множеств θi и βj образует данные, обладающие свойством «совместной аддитивности» (conjoint additivity). Правильное использование модели Раша позволяет отделить оценки испытуемых от оценок трудности заданий и наоборот. Это свойство Rasch Measurement носит название separability parameter estimates8 - «независимость оценок заданий от испытуемых и оценок испытуемых от параметров заданий».

На рис.1. показаны три характеристические кривые согласно уравнению (1) с трудностями заданий -2, 0 и +2 логита (первое самое легкое, второе - среднее, третье самое трудное). Из приведенных зависимостей видно, что чем выше уровень подготовленности θ испытуемого, тем выше вероятность успеха в том или ином задании.

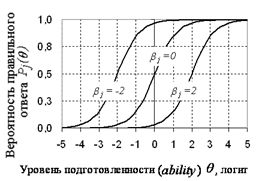
Рис.1. Характеристические кривые заданий (ICC) в модели (1PL).

Например, для испытуемого с θ =0 вероятность правильно ответить на первое задание близка к единице, на второе равна 1/2 и на третье почти равна нулю. Отметим, что в точках, где θ = β вероятность правильного ответа равна 0,5. То есть, если трудность задания равна уровню подготовленности (ability) испытуемого, то он с равной вероятностью может справиться или не справиться с этим заданием.

Характеристические (логистические) кривые для заданий теста в англо-язычной литература называются Item Characteristic Curve (ICC).

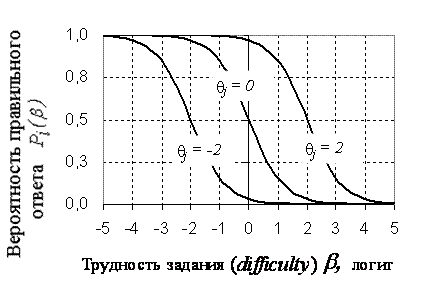
На рис.2. показаны три характеристические кривые испытуемых согласно уравнению (2) - «Person Characteristic Curve» (PCC). Показаны графики для трех испытуемых с уровнем подготовленности -2 логита (самый слабый), 0 логитов (средний) и +2 логита (сильный испытуемый).

Из приведенных зависимостей видно, что чем выше уровень подготовленности, тем выше вероятность правильного ответа на задание. Например, задание с трудностью b = 0 первый испытуемый ( q=-2) практически не сможет выполнить, второй q = 0) имеет вероятность выполнения задания равную 0,5, третий q=+2) легко справится с заданием, так как для него вероятность успеха почти равна единице.