Классические шкалы оценки знаний

В однопараметрической модели Раша заложено предположение о равнозначности всех заданий. Для коррекции этого предположения вводится дополнительный параметр , характеризующий различительную силу заданий. Отсюда получается исправленная модель вида

,

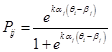известная под названием двухпараметрической IRT, или модели Бирнбаума. Для учёта поправок на угадывание Бирнбаум предложил учитывать ещё один дополнительный параметр и получил трёхпараметрическую модель вида

,

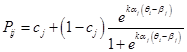где можно оценить, например, как вероятность случайного угадывания правильного ответа на соответствующий вопрос. Иногда также называют уровнем или коэффициентом псевдоуспеха, то есть вероятностью ответить на задание правильно для испытуемых с минимальной готовностью.

Очевидно, что при получается двухпараметрическая модель Бирнбаума, а при и — логистическая модель Раша.

Оценки параметров и обычно выполняются по известным статистическим приёмам, например, через построение подходящей функции правдоподобия. Известны также быстрые методы приближённой оценки этих параметров. При ясности вычислительных моделей IRT, однако, отмечены вопросы о содержательной интерпретации заложенных в них параметров. В частности, отмечены «краевые эффекты» этих моделей, это означает, что испытуемые, ответившие на все вопросы и не ответившие ни на один вопрос, не должны учитываться в общей статистике.

IRT считается общепризнанной, и обычно ставится вопрос только о калибровке по отношению к соответствующим параметрам.

Таким образом, центральной проблемой в оценке качества знаний оказывается проблема оценки субъективной когнитивной сложности или, как минимум, калибровка измерительного инструментария по критерию когнитивной сложности.

1) существуют латентные (скрытые) параметры личности, недоступные для непосредственного наблюдения. В тестировании это уровень подготовленность испытуемого и уровень трудности задания;

2) существуют индикаторные переменные, связанные с латентными параметрами, доступные для непосредственного наблюдения. По значениям индикаторных переменных можно судить о значениях латентных параметров;

3) оцениваемый латентный параметр должен быть одномерным. Это означает должен измерять знания только в одной, четко заданной, предметной области.

В качестве математической модели, связывающей успех испытуемого с уровнем его подготовленности и трудностью задания выбирается логистическая функция. Для модели Раша она имеет вид

(1)