Тематический план и методические рекомендации к проведению лекционных занятий

. (5)

В репере на прямой имеем координаты точек:

.

Поэтому

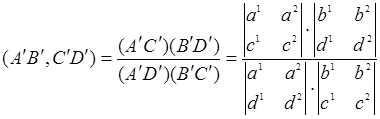
и, учитывая равенство (5),

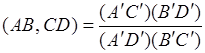. (6)

Аналогичные выражения получим, если прямая не проходит через вершину или координатного треугольника, проектируя точки прямой на из или на и из .

На проективной плоскости возьмем репер и произвольную точку . Пусть – проекции точек и на прямую из центра . Мы знаем, что в репере на прямой точка имеет координаты и, следовательно, по формуле (2) 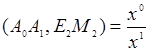при условии, что , то есть . Аналогичные выражения получим и для других отношений между координатами точки . Поэтому справедлива

Теорема 4.

Если точка имеет координаты относительно репера проективной плоскости, то отношение 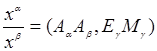равно сложному отношению четырех точек: двух вершин , и проекций , на прямую точек и из третьей вершины координатного треугольника (при условии, что , т. е. ) [3].

4.Итог занятия.

Итак, сегодня мы познакомились с понятием сложного отношения четырех точек прямой, изучили свойства сложного отношения, рассмотрели сложное отношение четырех прямых пучка.

– Как обозначается сложное отношение четырех точек прямой?

Возможный вариант ответа: (AB,CD).

– Какие свойства сложного отношения точек сегодня были изучены?

– Каким отношением связанно сложное отношение четырех точек прямой и отношение трех точек прямой?

– При обозначении сложного отношения точек важен порядок записи точек?