Тематический план и методические рекомендации к проведению лекционных занятий

Доказательство: 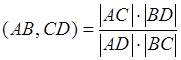, 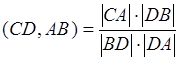. Учитывая, что получим, что . Свойство доказано.

20:Сложное отношение точек меняет свое значение на обратное, при перестановке точек внутри одной пары: .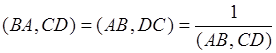

Доказательство: 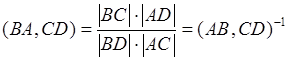, 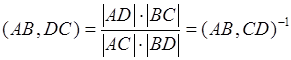. Свойство доказано.

30:

Если поменять местами точки внутри каждой пары, то сложное отношение не изменится: .

Доказательство: следует из свойства 20. 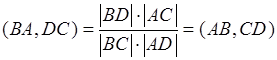. Свойство доказано.

40:.

Доказательства первого, второго и третьего свойства предложить студентам на самостоятельное изучение.

Замечание. Пусть на прямой заданы точки , тогда

1) тогда и только тогда, когда точки ,

2) тогда и только тогда, когда точки .

Теоремы о сложном отношении точек и прямых

Теорема 1. При любом проективном преобразовании плоскости сложное отношение четырех точек прямой сохраняется.

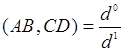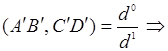
Доказательство. Пусть – проективное преобразование плоскости , прямая , ; точки переходят в отображении в точки . Как мы знаем, сужение есть проективное отображение . Это отображение вполне определяется упорядоченной парой реперов , где , . Если – координаты точки в репере , то эти же координаты имеет точка в репере . Но , . Теорема доказана.

Следствие. При любом проективном отображении одной прямой на другую сложное отношение четырех точек сохраняется.

Теорема 2.

Если биекция сохраняет сложное отношение любой четверки точек, то – проективное отображение.

Доказательство. Пусть – различные точки прямой и их образы в отображении . Существует единственной проективное отображение , которое переводит точки в точки соответственно.