Тематический план и методические рекомендации к проведению лекционных занятий

Если , и , то по доказанному

.(3)

Если , то по условию

(4)

(3), (4)

и, значит, точки и совпадают. Так как , то такой вывод справедлив для любой точки . Следовательно, данное нам отображение совпадает с проективным отображением . Теорема доказана.

Следствие. Биекция является проективным отображением тогда и только тогда, когда она сохраняет сложное отношение любой четверки точек.

Теорема 3.

Пусть – четыре различные прямые пучка П(О), прямая не проходит через точку и – точки пересечения этой прямой с прямыми . Тогда сложное отношение не зависит от выбора прямой (оно называется сложным отношением четырех названных прямых).

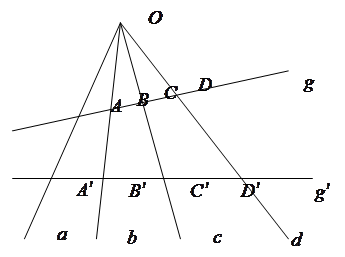
Рис. 2

Доказательство. Проведем еще какую-либо прямую , она пересекается с прямыми в точках соответственно (рис 2). Пучок П(О) устанавливает перспективное отображение по закону: . Так как это частный случай проективного отображения, то . Теорема доказана.

Следствие. Биекция :П()П() одного пучка на другой является проективным отображением тогда и только тогда, когда она сохраняет сложное отношение любой упорядоченной четверки прямых.

Как найти сложное отношение четырех точек прямой , зная их координаты , , , относительно репера на плоскости?

Прямая не проходит по крайней мере через одну из точек . Для определенности будем считать, что (рис. 3).

Рассмотрим перспективное отображение с помощью пучка прямых П(). Имеем: