Тематический план и методические рекомендации к проведению лекционных занятий

Лекция № 2

Тема: Полный четырехвершинник

Цель: обучающая: ввести определение гармонической четверки точек, изучить теорему о свойствах полного четырехвершинника;

развивающая: развивать память, логическое мышление, умение анализировать, выделять закономерности, обобщать, способность быстро ориентироваться в ситуации;

воспитательная: воспитывать положительное отношение к процессу обучения, уважение к сверстникам и преподавателю.

Тип занятия: лекция.

Структура занятия:

1.Организационный момент (2 мин).

2.Изложение нового материала (85 мин).

3.Итог занятия (3 мин).

Ход занятия

1.Организационный момент.

- преподаватель здоровается и отмечает отсутствующих студентов;

- сообщается тема занятия, его цель: На этой лекции мы познакомимся с понятием гармонической четверки точек, изучим теорему о свойствах полного четырехвершинника.

2. Изложение нового материала осуществляется с помощью традиционных методов обучения и слайдов по теме «Полный четырехвершинник», которые отражаются мультимедиа-проектором и содержат основной материал лекции.

Четверка точек прямой называется гармонической, если . Говорят также, что точки и гармонически сопряжены относительно точек и или что пары , и , гармонически разделяют одна другую. Точку называют при этом четвертой гармонической к упорядоченной тройке точек , , .

Из свойств сложного отношения четырех точек, заключаем, что в случае гармонической четверки точек , , , их сложное отношение не меняется только при перестановке пар точек, но и при перестановке точек одной пары:

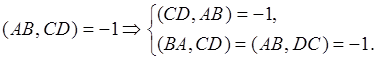
Аналогичными свойствами обладает и гармоническая четверка прямых пучка (которая определяется условием: ).

Пусть , , , – четыре точки общего положения на проективной плоскости. Если через каждые две из них провести прямую, то получим шесть прямых (рис. 4).

Фигура, образованная точками , , , и полученными шестью прямыми, называется полным четырехвершинником (или полным четырехугольником). Данные точки – его вершины, указанные прямые –его стороны.

Две стороны, не имеющие общей вершины, называются противоположными: и , и , и – пары противоположных сторон.