Тематический план и методические рекомендации к проведению лекционных занятий

Определение сложного отношения четырех точек прямой

Пусть точки лежат на одной прямой и заданы своими координатами: в некотором репере .

Определение. Сложным отношением упорядоченной четверки точек называется число равное

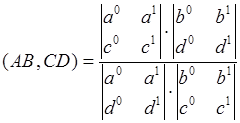. (1)

Коротко можно записать так 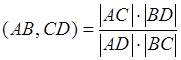, где определитель составленный из координат точек и .

Сложное отношение точек не зависит от выбора проективного репера. Если – собственные точки прямой, то выполняется равенство:

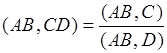. (2)

Пусть точки имеют координаты: , , . Поскольку проективные координаты определяются с точностью до проективного множества, то можно считать, что эти точки имеют координаты:

, , , . (*)

Где 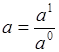, ,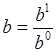,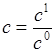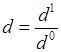. Поскольку, сложное отношение точек не зависит от выбора репера, то в качестве репера можно выбрать репер , тогда будут являться аффинными координатами на данной прямой.

Найдем простое отношение (используя определение простого отношения): , .

Найдем сложное отношение по формуле (1), используя координаты (*):

.

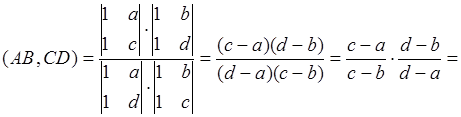
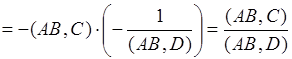Замечание 1. Несобственная точка делит любой отрезок прямой в отношении , то есть .

Замечание 2. Если выбрать в качестве репера , то в этом репере точка будет иметь координаты: . Зная сложное отношение точек , всегда можно найти расположение точки на прямой. В этом случае .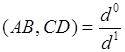

Значит, если , то .

Свойства сложного отношения четырех точек

10:

Сложное отношение точек не изменится, если поменять местами пару точек: .