Тематический план и методические рекомендации к проведению практических занятий

Тема:

«Сложное отношение четырех точек».

Цель:

сформировать умения и навыки применения на практике теоретического материала, данного на лекции.

Задачи:

1) образовательная – формирование научного мировоззрения;

2) развивающая – развитие у обучаемых умения обобщать, систематизировать полученные знания;

3) воспитательная – воспитания познавательного интереса обучаемых, коммуникативных качеств, умения слушать, культуры межличностных взаимоотношений, аккуратности в работе, трудолюбия.

Оборудование:

доска, мультимедиапроектор, компьютер.

Структура практического занятия:

1) организационный момент (5 мин.);

2) актуализация знаний по данной теме (5 мин.);

3) закрепление теоретического материала на практике (70 мин.);

4) запись домашнего задания (7 мин.);

5) подведение итогов практического занятия (3 мин.).

Ход практического занятия:

1. Организационный момент.

Сообщается тема практического занятия и записывается на доске, в тетради.

2. Актуализация знаний по данной теме.

Задаются вопросы, необходимые для проведения данного практического занятия, рассмотренные на лекционном занятии (основные понятия и формулы).

1) Что называется сложным отношением четырех точек прямой?

– Сложным отношением четырех точек лежащих на одной прямой называется число:

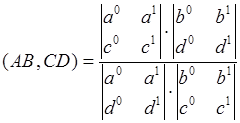
2) Свойства сложного отношения точек

– 10:

Сложное отношение точек не изменится, если поменять местами пару точек: .

– 20:

Сложное отношение точек меняет свое значение на обратное, при перестановке точек внутри одной пары: .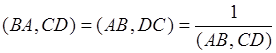

– 30:

Если поменять местами точки внутри каждой пары, то сложное отношение не изменится: .

– 40:

3) Каким отношением определяется связь сложного отношения точек с простым?

–

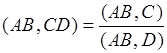
3. Закрепление теоретического материала на практике.

На этом этапе проведения занятия используется методика коллективных способов обучения. К занятию заранее приготовлено пять видов карточек. Пять задач, в каждой из которых содержится пара однотипных заданий. Каждой задаче соответствует свой номер. Каждый из студентов получает номер задачи и приступает к её решению. После того как все студенты, по мере своих сил справились с заданиями, группа разбивается на пары. Работая в парах студенты проверяют правильность решения задачи напарником, объясняя решение своего задания подробно, если у другого возникли затруднения при решении задания напарника. Проверив друг у друга правильность решения задач и оформив решение в тетрадь, напарники расходятся. На этом их работа в данной паре заканчивается, пара распадается, а каждый из них ищет себе нового напарника.