Контрольно-измерительные материалы и интерпретация результатов тестирования

(3)

Для рассматриваемого примера

Стандартное отклонение не следует путать со средним отклонением, последнее находится по формуле

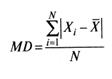(4)

и является средним значением суммы отклонений, взятых по модулю.

Интерпретация. Дисперсия играет важную роль в оценке качества нормативно-ориентированных тестов. Слабая вариация результатов испытуемых указывает на низкое качество теста. Основания для подобного вывода вполне прозрачны. Низкая дисперсия индивидуальных баллов говорит о слабой дифференциации испытуемых по уровню подготовки в тестируемой группе, т.е. о той ситуации, которая диаметрально противоположна основной цели создания нормативно-ориентированного теста.

Излишне высокая дисперсия, характерная для случая, когда все учащиеся отличаются по числу выполненных заданий, также грозит неприятными последствиями и требует переработки теста. Превышение разумных пределов величины дисперсии приводит к искажению вида распределения, которое начинает существенно отличаться от планируемой теоретической нормальной кривой.

При переработке теста следует руководствоваться простым правилом: если проверка согласованности эмпирического распределения с нормальным дает положительные результаты, а дисперсия растет, то это означает, что происходит повышение дифференцирующей способности теста и процесс улучшения теста.

Конечно, использовать какой-либо из существующих критериев для проверки нормальности распределения в практике довольно неудобно. Поэтому зачастую непрофессионалы в оценке характера распределения руководствуются простым соотношением. Для этого величину X сравнивают с утроенным стандартным отклонением. Если это равенство выполняется, т.е. если

??,

то дисперсия оптимально высока и можно принять гипотезу о нормальности распределения.

??

нормальной кривой, оценивается с помощью асимметрии. Наличие асимметрии легко установить визуально, анализируя полигон частот или гистограмму. Более тщательный анализ можно провести с помощью обобщенных статистических характеристик, предназначенных для оценки асимметрии в распределении.

На рис. 2.9 представлены кривые распределения с отрицательной, нулевой и положительной асимметрией (слева направо) соответственно

Рис.2.9. Отрицательная, нулевая, положительная асимметрия.

Наиболее удачная формула для подсчета асимметрии имеет вид

Асимметрия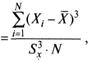 (5)

где– индивидуальный балл i-го ученика; – среднее значение баллов по тестируемой группе; – куб стандартного отклонения; N – число учеников. После подстановки данных из рассматриваемого выше примера (табл. 3) величина асимметрии будет равна

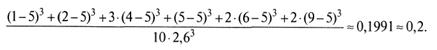
Интерпретация. При интерпретации полученного значения асимметрии 0,2 необходимо обратить внимание на то, что вклад положительных значений кубов разностей будет больше кубов отрицательных значений, но ненамного, поэтому величинa асимметрии получилась положительной и небольшой. Таким образом, асимметрия распределения положительна, если основная часть значений индивидуальных баллов лежит справа от среднего значения, что обычно характерно для излишне легких тестов. Асимметрия распределения баллов отрицательна, если большинство учеников получили оценки ниже среднего балла. Эффект отрицательной асимметрии встречается в излишне трудных тестах, не сбалансированных правильно по трудности при отборе заданий в тест.

В хорошо сбалансированном по трудности тесте, как уже отмечалось ранее, распределение баллов имеет вид нормальной кривой. Для нормального распределения характерна нулевая асимметрия, что вполне естественно, так как при полной симметрии каждое значение балла, меньшее , уравновешивается другим симметричным, большим, чем .

Эксцесс. С помощью эксцесса можно получить представление о том, являются ли полигон частот или гистограмма островершинными или плоский. На рис. 2.10 изображены три кривые, отличающиеся по эксцессу.

Рис. 2.10. Островершинная, средневершинная и плоская кривые.

Первая кривая (А) – островершинная, имеет явно выраженный положительный эксцесс, вторая кривая (В) – средневершинная, имеет нулевой эксцесс, характерный для нормальной кривой, третья кривая (С) – плосковершинная, кривые такого типа имени эксцесс меньше нуля.

Обычно эксцесс вычисляется по формуле