Контрольно-измерительные материалы и интерпретация результатов тестирования

Среднее выборочное (среднее арифметическое) определяется суммированием всех значений совокупности и последующим делением на их число. Для совокупности индивидуальных баллов ??

Х2, ., XN группы ?? испытуемых среднее значение X будет

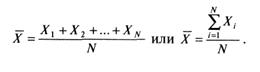(1)

Среднее арифметическое индивидуальных баллов испытуемых для рассматриваемого выше примера матрицы (табл.3 или 4) будет

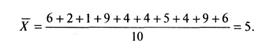
Вычисление среднего значения легко произвести на любом калькуляторе или ПЭВМ. Процесс вычисления значительно упрощается, если отдельные значения в совокупности повторяются, как, например, в табл. 7. Для данных таблицы сумма всех результатов определяется умножением каждого значения балла на его частоту и последующим суммированием полученных произведений. Тогда среднее значение будет

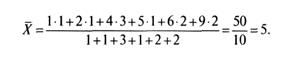
В отличие от моды на величину среднего влияют значения всех результатов. Таким образом, среднее арифметическое характеризует всю совокупность значений. Оно обобщает индивидуальные особенности составляющих распределения, в нем уравниваются отдельные значения рассматриваемой величины.

Получаемые результаты в процессе разработки теста требуют специальной интерпретации и размышления.

Интерпретация мер центральной тенденции. Меры центральной тенденции в определенной степени помогают при оценке качества теста в том случае, когда она проводится по результатам апробации теста на репрезентативной выборке учеников. Обычно считают, что хороший нормативно-ориентированный тест обеспечивает нормальное распределение индивидуальных баллов репрезентативной выборки учеников, когда среднее значение баллов находится в центре распределения, а остальные значения концентрируются вокруг среднего по нормальному закону, т.е. примерно 70% значений в центре, а остальные сходят «на нет» к краям распределения, как на рис. 2.5.

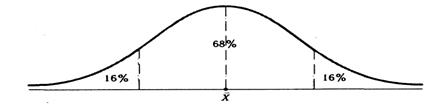
Рис. 2.5. Нормальная кривая распределения индивидуальных баллов

Если тест обеспечивает близкое к нормальному распределение баллов, то это означает, что на его основе можно определить устойчивое среднее значение баллов, которое принимается в качестве одной из репрезентативных норм выполнения теста. Обратный вывод, вообще говоря, неверен: устойчивость тестовых норм вовсе не предполагает обязательного нормального распределения эмпирических результатов выполнения теста.

Может сложиться представление о том, что существует жесткая связь между нормальным распределением частот и практически любыми эмпирическими данными по тесту.

На самом деле это не так, поскольку нормальная кривая – это изобретение математиков, которое в сглаженном, идеальном виде описывает реальный полигон частот. На практике никогда не была и не будет получена совокупность данных, распределенных точно по нормальному закону. Просто иногда полезно, допуская определенную ошибку, утверждать, что эмпирические данные распределены по нормальному закону, и описывать полигон частот сглаженной кривой.

Нормальное распределение унимодально и симметрично, т.е. половина результатов, расположенная ниже моды, в точности совпадает с другой половиной, расположенной выше, а мода и среднее значение равны. Отсутствие полной симметрии в полигоне частот на практике приводит к смещению моды относительно среднего значения.

В малых выборках мода, как и среднее значение, теряет свою стабильность, хотя причиной нестабильности может служить и неправильный подбор по трудности заданий в тесте. Например, если по репрезентативной выборке получилась гистограмма с бимодальным распределением (рис. 2.6), то среднее значение распределения, находящееся в центре, никак не может служить нормой выполнения теста. Скорее всего, тест был сконструирован неудачно, что послужило причиной отсутствия нормального распределения эмпирических результатов выполнения теста.

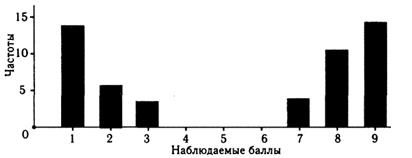
Рис. 6. Гистограмма бимодального распределения

Смещение среднего значения влево или вправо, как на рис. 2.7 и 2.8, говорит о слишком трудной либо соответственно слишком легкой подборке заданий теста.

Таким образом, правильно сконструированный нормативно-ориентированный тест на репрезентативной выборке учеников должен обеспечивать близкое к симметричному распределению индивидуальных баллов, когда мода и среднее значение примерно равны, а остальные результаты расположены вокруг среднего по нормальному закону.

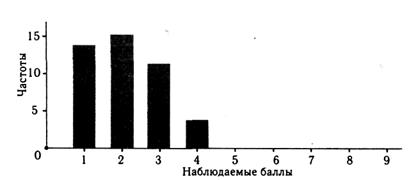
Рис. 7. Гистограмма распределения баллов по трудному тесту

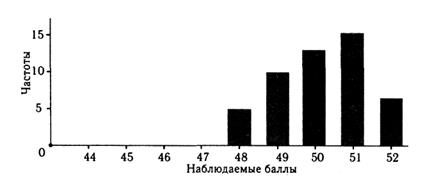
Рис. 8. Гистограмма распределения баллов по легкому тесту

Седьмой шаг. На седьмом шаге определяются описательные характеристики, служащие мерами изменчивости в группе данных по тесту. Введение характеристик связано с необходимостью выявления дополнительных оснований для обоснованного сравнения различных распределений по тестам. При сравнении нескольких распределений с одинаковыми средними с помощью дополнительных характеристик можно выявить существенные различия в структуре, указывающие на значительные отличия в качестве тестов.