Контрольно-измерительные материалы и интерпретация результатов тестирования

Наиболее важная характеристика указывает на особенности разброса эмпирических данных вокруг среднего значения баллов по тесту. Отдельные значения индивидуальных баллов могут быть тесно сгруппированы вокруг своего среднего балла либо, наоборот, сильно удалены от него. Поэтому необходимы оценки характеристик распределения, отражающие вариацию, или, как говорят иначе, изменчивость баллов по тесту.

Для характеристик степени рассеяния отдельных значений вокруг среднего используются различные меры: размах, дисперсия, стандартное отклонение.

Размах измеряет на шкале расстояние, в пределах которого изменяются все значения показателя в распределении. Например, распределения индивидуальных баллов табл. 6 размах равен ??.

Вариационный размах легко вычисляется, но используется крайне редко при характеристике распределения баллов по тесту. И для этого есть веские основания. Во-первых, размах является весьма приближенным показателем, так как не зависит от степени изменчивости промежуточных значений, расположенных между крайними значениями в распределении баллов по тесту. Во-вторых, крайние значения индивидуальных баллов, как правило, ненадежны, поскольку содержат в себе значительную ошибку измерения. В этой связи более удачной мерой считается дисперсия.

Дисперсия. Подсчет дисперсии основан на вычислении отклонений каждого значения показателя от среднего арифметического в распределении. Для индивидуальных баллов значения отклоненийнесут информацию о вариации совокупности значений баллов N учеников, т. е. отражают меру неоднородности результатов по тесту. Совокупность с большей неоднородностью будет иметь большие по модулю отклонения, наоборот, для однородных распределений отклонения должны быть близки к нулю. Знак отклонения указывает место результата ученика по отношению к среднему арифметическому по тесту. Для ученика с индивидуальным баллом выше среднего значение разности будет положительно, а для тех, у кого результат ниже, отклонение меньше нуля.

Например, в распределении баллов со средним значением из табл. 6 отклонения будут:

для 3-го ученика

для 2-го ;

для 5-, 6-и 8-го ;

для 7-го ;

для 1- и 10-го ;

для 4- и 9-го .

Если просуммировать все отклонения, взятые со своим знаком, то для симметричных распределений сумма будет равна нулю. В рассматриваемом примере сумма отклонений

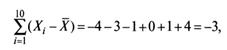
что, конечно, не позволяет оценить меру неоднородности распределения, поскольку отрицательные и положительные слагаемые уничтожают друг друга. Для преодоления этого эффекта каждое отклонение возводят в квадрат и находят сумму квадратов отклонений: Тогда сумма вида

будет большой, если результаты тестирования отличаются существенной неоднородностью, и малой – в случае близких результатов испытуемых по тесту.

Для рассматриваемого примера

Величина суммы зависит также от размера выборки учеников, выполнявших тест. Зависимость здесь вполне очевидна: чем больше учеников, тем больше положительных слагаемых в сумме, характеризующей вариацию баллов по тесту. Поэтому при сравнении мер изменчивости распределений, отличающихся по объему, возникает препятствие, которое снимается путем деления каждой суммы на N-1, где N – число учеников, выполнявших тест. Определяемая таким образом мера изменчивости называется дисперсией. Она обычно обозначается символом и вычисляется по формуле

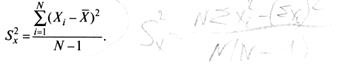(2)

Для рассматриваемого примера

В примере вычислялась просто в силу того, что среднее арифметическое было целым числом. На практике, как правило, приходится иметь дело с дробными значениями , что делает использование формулы (2) крайне утомительным.

Стандартное отклонение. Кроме дисперсии, для характеристики меры изменчивости распределения удобно использовать еще один показатель вариации, который называется стандартным отклонением. Стандартное отклонение равно корню квадратному из дисперсии: